leetcde刷题笔记——栈队列堆

剑指offer中的栈队列堆部分。

1.栈的压入、弹出序列

用一个栈来模拟。

若栈顶等于popped[j]，则弹出，否则将pushed[i]压入。

2.最小的k个数

【法一】排序

• 时间复杂度$O(nlog n)$
• 空间复杂度$O(logn)$

【法二】维护大顶堆

首先将前k个数插入大顶堆，从第k+1个数开始，若当前数小于堆顶，则弹出堆顶，将当前树插入。

• 时间复杂度$O(nlog n)$
• 空间复杂度$O(k)$

【法三】快排思想

3.**数据流中的中位数

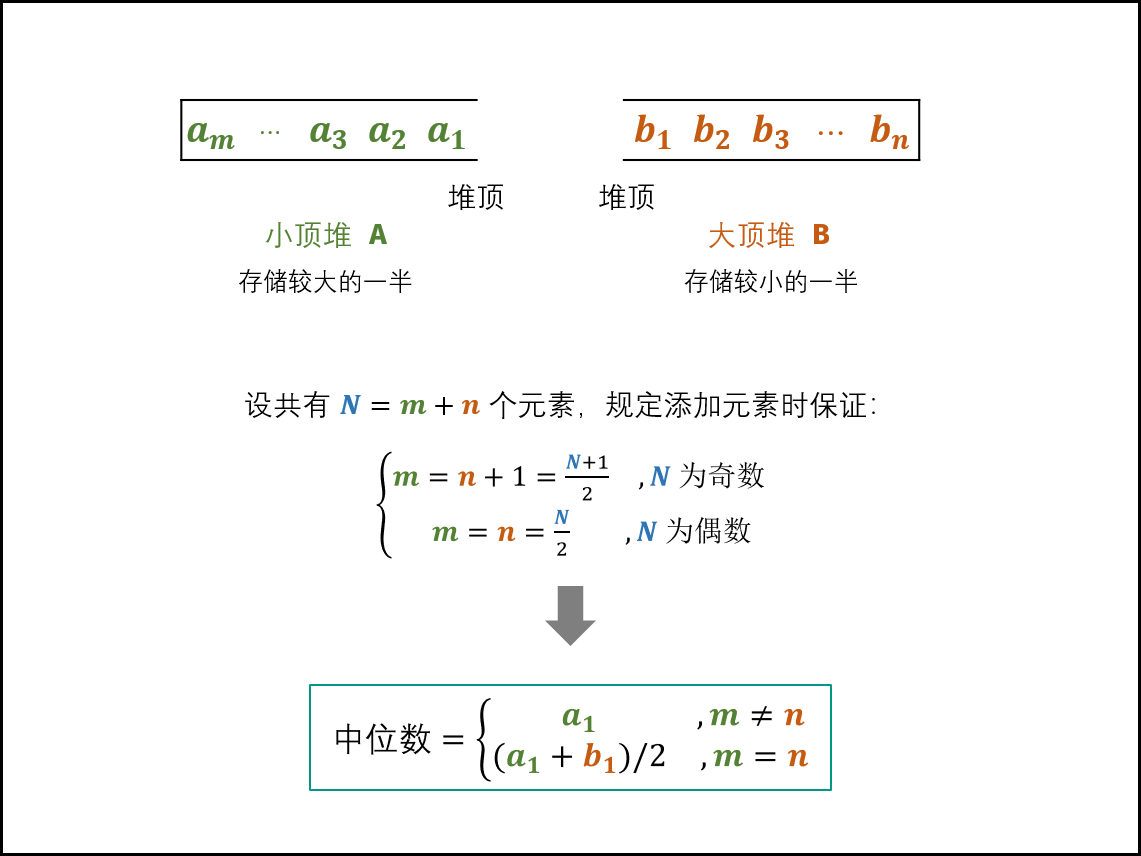
建立一个小顶堆A和大顶堆B，各保存列表的一般元素，且规定：

• A保存 较大 的一半，长度为$\frac{N}{2}$(N为偶数)或$\frac{N+1}{2}$(N为奇数)；
• B保存 较小 的一半，长度为$\frac{N}{2}$(N为偶数)或$\frac{N-1}{2}$(N为奇数)；
• 随后，中位数可以仅根据A, B的堆顶元素计算得到。

class MedianFinder {
public:
    /** initialize your data structure here. */
    priority_queue<int,vector<int>,greater<int> > minHeap;
    priority_queue<int,vector<int>,less<int> > maxHeap;
    MedianFinder() {

    }
    
    void addNum(int num) {
        if (minHeap.size()==maxHeap.size()){
            maxHeap.push(num);
            minHeap.push(maxHeap.top());
            maxHeap.pop();
        }
        else{
            minHeap.push(num);
            maxHeap.push(minHeap.top());
            minHeap.pop();
        }
    }
    
    double findMedian() {
        if (minHeap.size()==maxHeap.size()&&minHeap.size()!=0){
            return double(minHeap.top()+maxHeap.top())*0.5;
        }
        else{
            return minHeap.top();
        }
    }
};

4.*滑动窗口

用deque维护非严格递减元素。

• deque 内仅包含窗口内的元素 ⇒ 每轮窗口滑动移除了元素 nums[i -1]，需将 deque 内的对应元素一起删除。
• deque 内的元素 非严格递减 ⇒ 每轮窗口滑动添加了元素 nums[j+1]，需将 deque 内所有 < nums[j + 1] 的元素删除。